Advertisements
Advertisements
प्रश्न
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
उत्तर
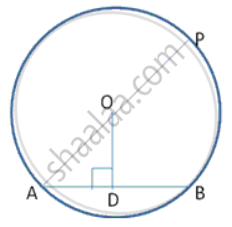
AD = DB = 1.6 cm (Perpendicular from centre to a chord bisects the chord)
In right Δ ODA ,
By Pythagoras theorem , OA2 = OD2 + AD2
= 1.62 + 1.22
= 2.56 + 1.44
OA2 = 4
OA = 2 cm
Diameter (AP) = 2 (OA) = 2 (1) = 4 cm
APPEARS IN
संबंधित प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

Say true or false:
Two diameters of a circle will necessarily intersect.
