Advertisements
Advertisements
प्रश्न
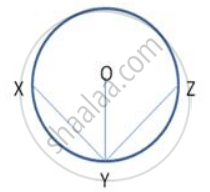
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
उत्तर

Join OX and OZ
In Δ XOY and Δ ZOY
OX = YZ (radii of same circle)
XY = YZ (given)
OY = OY (common)
∴ Δ XOY ≅ Δ ZOY (SSS)
∴ ∠ OYX = ∠ OYZ (CPCT)
Hence , OY is the bisector of ∠XYZ passing through O.
APPEARS IN
संबंधित प्रश्न
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
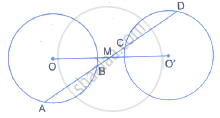
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
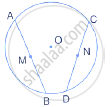
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
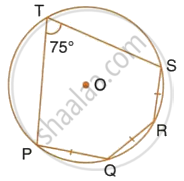
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
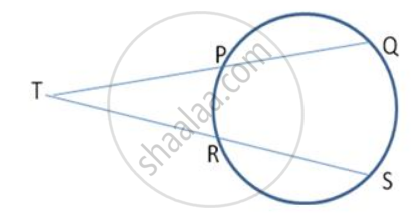
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
In fig, AB and CD are two equal chords of a circle with centre O. If M and N are the midpoints of AB and CD respectively,
prove that (a) ∠ ONM = ∠ ONM (b) ∠ AMN = ∠ CNM.
AB and AC are two equal chords of a circle with centre o such that LABO and LCBO are equal. Prove that AB = BC.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP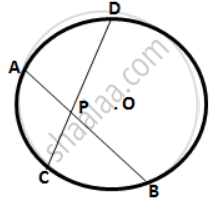
Prove that equal chords of congruent circles subtend equal angles at their center.
