Advertisements
Advertisements
प्रश्न
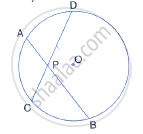
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP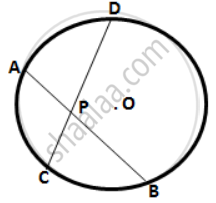
उत्तर
Drop OM and ON perpendicular on AB and CD.
Join OP, OB, and OD.
∴ OM and ON bisect AB and CD respectively. ....( Perpendicular drawn from the centre of a circle to a chord bisects it. )
∴ MB = `1/2"AB" = 1/2"CD" = "ND"`....(i)
In right ΔOMB,
OM2 = OB2 - MB2 ....(ii)
In right ΔOND,
ON2 = OD2 - ND2 ....(iii)
From (i), (ii), and (iii),
OM = ON
In ΔOPM and ΔOPN,
∠OMP = ∠ONP ....( both 90° )
OP = OP ....( common )
OM = ON ....( proved above )
By Right Angle-Hypotenuse-Side criterion of congruence,
∴ ΔOPM ≅ ΔOPN ....( by RHS )
The corresponding parts of the congruent triangles are congruent.
∴ PM = PN ....( c.p.c.t. )
Adding (i) to both sides,
MB + PM = ND + PN
⇒ BP = DP
Now, AB = CD
∴ AB - BP = CD - DP ...( ∵ BP = DP )
⇒ AP = CP.
APPEARS IN
संबंधित प्रश्न
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
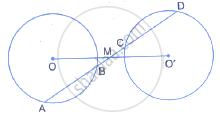
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
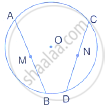
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
Two equal chords AB and CD of a circle with centre O, intersect each other at point P inside the circle, prove that:
(i) AP = CP,
(ii) BP = DP
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
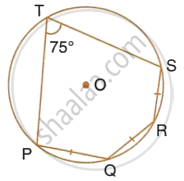
The given figure shows a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
- ∠POS,
- ∠QOR,
- ∠PQR.
Two congruent drdes have their centres at 0 and P. Mis the midpoint of the line segment OP. A straight line is drawn through M cutting the two circles at the points A, B, C and D. Prove that the chords AB and CD are equal.
In fig., chords AB and CD of a circle intersect at P. AP = 5cm, BP= 3cm and CP = 2.5cm. Determine the length of DP.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.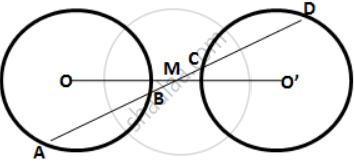
In the adjoining diagram, chords AB, BC and CD are equal. O is the centre of the circle. If ∠ ABC = 120°, Calculate: (i) ∠ BAC, (ii) ∠ BEC, (iii) ∠ BED, (iv) ∠ COD