Advertisements
Advertisements
प्रश्न
Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle.
Prove that: (i) AP = CP ; (ii) BP = DP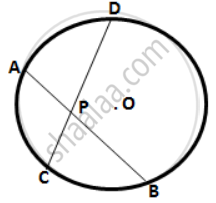
उत्तर
Drop OM and ON perpendicular on AB and CD.
Join OP, OB, and OD.
∴ OM and ON bisect AB and CD respectively. ....( Perpendicular drawn from the centre of a circle to a chord bisects it. )
∴ MB = `1/2"AB" = 1/2"CD" = "ND"`....(i)
In right ΔOMB,
OM2 = OB2 - MB2 ....(ii)
In right ΔOND,
ON2 = OD2 - ND2 ....(iii)
From (i), (ii), and (iii),
OM = ON
In ΔOPM and ΔOPN,
∠OMP = ∠ONP ....( both 90° )
OP = OP ....( common )
OM = ON ....( proved above )
By Right Angle-Hypotenuse-Side criterion of congruence,
∴ ΔOPM ≅ ΔOPN ....( by RHS )
The corresponding parts of the congruent triangles are congruent.
∴ PM = PN ....( c.p.c.t. )
Adding (i) to both sides,
MB + PM = ND + PN
⇒ BP = DP
Now, AB = CD
∴ AB - BP = CD - DP ...( ∵ BP = DP )
⇒ AP = CP.
APPEARS IN
संबंधित प्रश्न
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O’
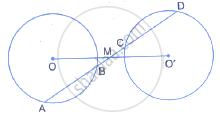
Prove that the chords AB and CD, which are intercepted by the two circles are equal.
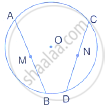
M and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. prove that:
(i) ∠BMN = ∠DNM.
(ii) ∠AMN = ∠CNM.
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O. If the radius of the circle is 10 cm, find the area of the rhombus.
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
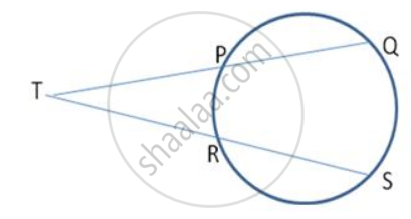
In fig. the centre of the circle is O. PQ and RS are two equal chords of the circle which , when produced , meet at T outside the circle . Prove that (a) TP = TR (b) TQ = TS.
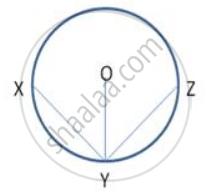
In following figure .,XY and YZ are two equal chords of a circle with centre O. Prove that the bisector of ∠ XYZ passes through O.
In the given Figure, AB and CD are two chords of a circle, intersecting each other at P such that AP = CP. Show that AB= CD.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'. Prove that the chords AB and CD, which are intercepted by the two circles, are equal.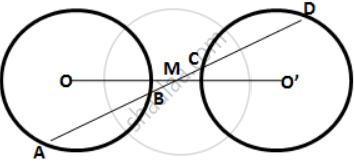
Prove that equal chords of congruent circles subtend equal angles at their center.
Two equal circles intersect in P and Q. A straight line through P meets the circles in A and B. Prove that QA = QB
