Advertisements
Advertisements
प्रश्न
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
उत्तर
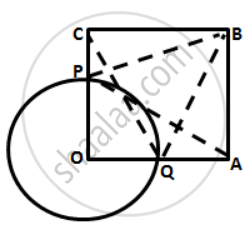
(i) In ΔOPA and ΔOQC,
OP = OQ ....[ radii of same circle ]
∠AOP = ∠COQ ... [ both 90° ]
OA = OC ... [ sides of the square ]
By Side- Angle - Side criterion of congruence.
∴ ΔOPA ≅ ΔOQC ...[ by SAS ]
(ii) Now, OP = OQ ...[ radii ]
and OC = OA ...[ sides of the square ]
∴ OC - OP = OA - OQ
⇒ CP = AQ ....(i)
In ΔBPC and ΔBQA,
BC = BA ...[ sides of the square ]
∠PCB = ∠QAB ...[ both 90° ]
PC = QA ...[ by ( i ) ]
By Side- Angle-Side criterion of congruence,
∴ ΔBPC ≅ ΔBQA ...[ by SAS ]
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Draw circle with the radii given below.
2 cm
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?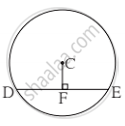
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
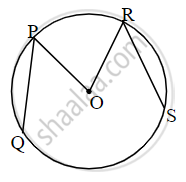
From the figure, identify a chord.

Is every chord of a circle also a diameter?
