Advertisements
Advertisements
प्रश्न
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

उत्तर
The given figure is below
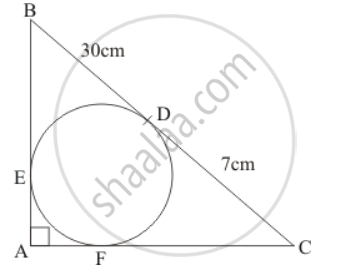
(i) The given triangle ABC is a right triangle where side BC is the hypotenuse. Let us now apply Pythagoras theorem. We have,
`AB^2+AC^2=BC^2`
Looking at the figure we can rewrite the above equation as follows.
`(BE+EA)^2+(AF+FC)^2=(30+7)^2` …… (1)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have the following,
BE = BD
It is given that BD = 30 cm. Therefore,
BE = 30 cm
Similarly,
CD = FC
It is given that CD = 7 cm. Therefore,
FC = 7 cm
Also, on the same lines,
EA = AF
Let us substitute these in equation (1). We get,
`(BE+EA)^2+(AF+FC)^2=(30+7)^2`
`(30+AF)^2+(AF+7)^2=37^2`
`(30^2+2 xxAF+AF^2)+(AF^2+2xx7xxAF+7^2)=1369`
`900+60AF+AF^2+AF^2+14AF+49=1369`
`2F^2+74AF-420=0`
`AF^2+37AF-210=0`
`AF^2(AF+42)-5(AF+42)=0`
`AF(AF+42)-5(AF+42)=0`
`(AF-5)(AF+42)=0`
Therefore,
Therefore,
AF = 5
Or,
AF = − 42
Since length cannot have a negative value,
AF = 5
APPEARS IN
संबंधित प्रश्न
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

One chord of a circle is known to be 10 cm. The radius of this circle must be
Twice the radius is ________________
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
