Advertisements
Advertisements
प्रश्न
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

उत्तर
Let us join the point of contact E with the centre of the circle say O. Also, let us join the point of contact F with the centre of the circle O. Now we have a quadrilateral AEOF.
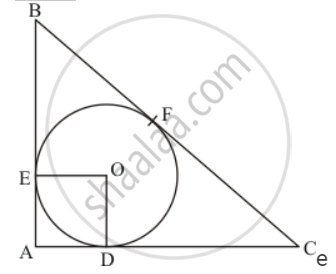
In this quadrilateral we have,
`∠EAD = 90^0`(Given in the problem)
`∠oda = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
`∠OEA = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠EAD + ∠ ODA + ∠ EOD + ∠ OEA = 360^o`
`90^0+90^o +90^o + ∠EOD = 360^o`
` ∠EOD = 90^o`
Since all the angles of the quadrilateral are equal to 90° and the adjacent sides are equal, this quadrilateral is a square. Therefore all the sides are equal. We have found that
AF = 5
Therefore,
OD = 5
OD is nothing but the radius of the circle.
Thus we have found that AF = 5 cm and radius of the circle is 5 cm.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

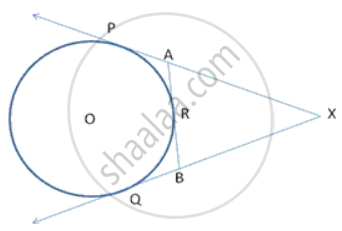
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.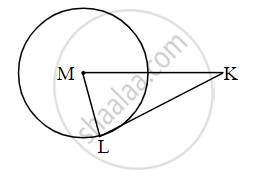
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.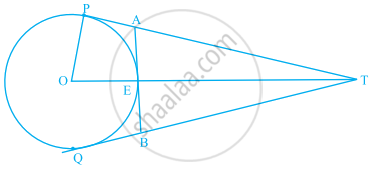
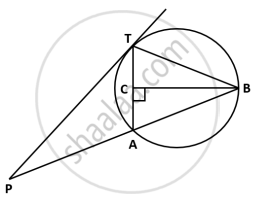
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
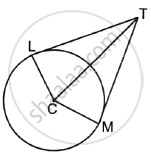
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
