Advertisements
Advertisements
प्रश्न
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
उत्तर
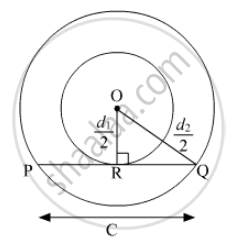
Let O be the centre of two concentric circles and PQ be the tangent to the inner circle that touches the circle at R.
Now, OQ= \[\frac{1}{2} d_2\] and
OR=\[\frac{1}{2} d_1\]
Also, PQ = c
As, PQ is the tangent to the circle.
⇒ OR ⊥ PQ
⇒ QR =\[\frac{1}{2}PQ = \frac{1}{2}c\]
In Triangle OQR,
∴ By Pythagoras Theorem,
\[\left( OQ \right)^2 = \left( OR \right)^2 + \left( RQ \right)^2 \]
\[ \Rightarrow \left( \frac{d_2}{2} \right)^2 = \left( \frac{d_1}{2} \right)^2 + \left( \frac{c}{2} \right)^2 \]
\[ \Rightarrow \left( d_2 \right)^2 = \left( d_1 \right)^2 + c^2\]
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
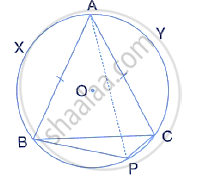
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
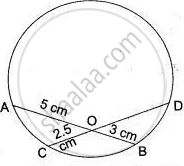
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
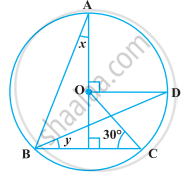
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
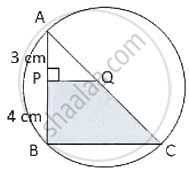
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.