Advertisements
Advertisements
प्रश्न
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
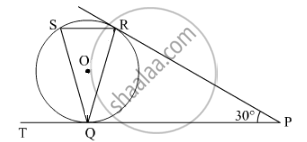
In the given figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the measure of ∠RQS.
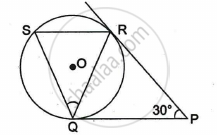
उत्तर
It is given that, ∠RPQ = 30° and PQ and PR are tangents drawn to a circle from P to the same circle.
∴ PQ = PR ...(Tangents drawn from an external point to a circle are equal in length.)
In ∆PQR,
PQ = PR
∴ ∠PQR = ∠PRQ ...(Angles opposite to equal sides are equal.)
Now, In ∆PQR,
∠PQR + ∠PRQ + ∠RPQ = 180° ...(Angle sum property of a triangle)
∴ ∠PQR + ∠PQR + 30° = 180°
∴ 2∠PQR + 30° = 180°
∴ 2∠PQR = 180° − 30°
∴ 2∠PQR = 150°
∴ ∠PQR = 75°
So, ∠PQR = ∠QRS = 75° ...(Alternate angles)
∠PQR = ∠QSR = 75° ...(Alternate segment angles are equal)
and ∠QRS = ∠QSR = 75°
∴ ΔQRS is also an isosceles triangle.
∴ ∠QRS + ∠QSR + ∠RQS = 180°
∴ 75° + 75° + ∠RQS = 180°
∴ ∠RQS = 180° − 150°
∴ ∠RQS = 30°
APPEARS IN
संबंधित प्रश्न
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Draw circle with the radii given below.
4 cm
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

