Advertisements
Advertisements
प्रश्न
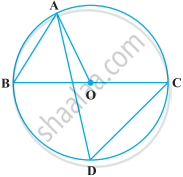
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

पर्याय
35°
45°
55°
65°
उत्तर
55°

`angleBAD = angleBCD = 35°` (Angle in the same segment are equal.)
Also, since the chords ‘AD’ and ‘BC’ intersect perpendicularly we have,
`angleCPD = 90°`
Consider the triangle ΔCPD ,
`angleCPD + anglePDC + anglePCD = 180°`
`anglePDC = 180° - anglePCD - angleCPD`
= 180° - 35° - 90°
= 55°
`anglePDC = angleADC = 55°`
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
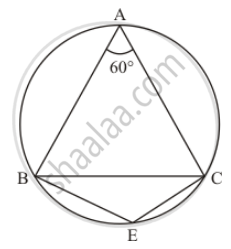
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

The circle which passes through all the vertices of a triangle is called ______.
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
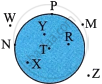 |
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.