Advertisements
Advertisements
Question
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Options
35°
45°
55°
65°
Solution
55°

`angleBAD = angleBCD = 35°` (Angle in the same segment are equal.)
Also, since the chords ‘AD’ and ‘BC’ intersect perpendicularly we have,
`angleCPD = 90°`
Consider the triangle ΔCPD ,
`angleCPD + anglePDC + anglePCD = 180°`
`anglePDC = 180° - anglePCD - angleCPD`
= 180° - 35° - 90°
= 55°
`anglePDC = angleADC = 55°`
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
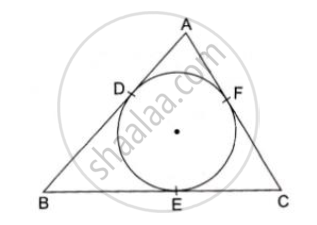
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
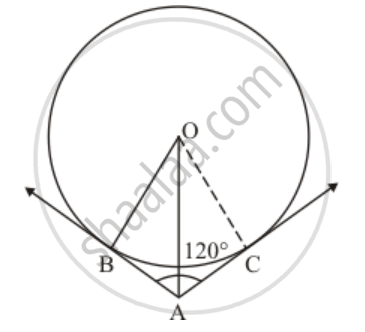
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.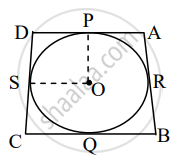
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
