Advertisements
Advertisements
Question
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
Options
60 cm2
65 cm2
30 cm2
32.5 cm2
Solution
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is 60 cm2.
Explanation:
Firstly, draw a circle of radius 5 cm with centre O.
P is a point at a distance of 13 cm from O.
A pair of tangents PQ and PR are drawn.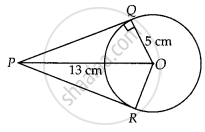
Thus, quadrilateral PQOR is formed.
∵ OQ ⊥ QP ...[Since, QP is a tangent line]
In right angled ∆PQO,
OP2 = OQ2 + QP2
⇒ 132 = 52 + QP2
⇒ QP2 = 169 – 25 = 144
⇒ QP = 12 cm
Now, area of ∆OQP
= `1/2 xx "QP" xx "QO"`
= `1/2 xx 12 xx 5`
= 30 cm2
∴ Area of quadrilateral PQOR
= 2 × ar ∆OQP
= 2 × 30
= 60 cm2
APPEARS IN
RELATED QUESTIONS
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Prove that the tangents at the extremities of any chord make equal angles with the chord.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

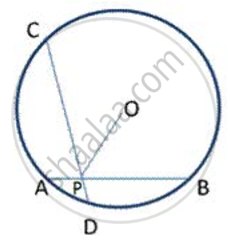
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.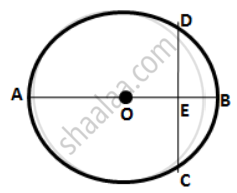
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Find the diameter of the circle
Radius = 6 cm
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]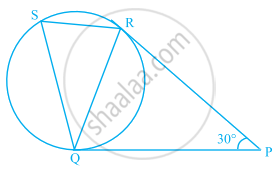
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
