Advertisements
Advertisements
Question
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Solution
From the given figure, we have
TP = TQ (Two tangents, drawn from an external point to a circle, have equal length.)
and
∠TQO=∠TPO=90° (Tangent to a circle is perpendicular to the radius through the point of contact.)
In ∆TOQ,
QT2+OQ2=OT2
⇒QT2=132−52=144
⇒QT=12 cm
Now,
OT − OE = ET = 13 − 5 = 8 cm
Let QB = x cm.
∴ QB = EB = x (Two tangents, drawn from an external point to a circle, have equal length.)
Also,
∠OEB = 90° (Tangent to a circle is perpendicular to the radius through the point of contact.)
In ∆TEB,
EB2+ET2=TB2
⇒x2+82=(12−x)2
⇒x2+64=144+x2−24x
⇒24x=80
`=>x = 80/24=10/3`
`:.AB=2x=20/3cm`
Thus, the length of AB is `20/3 cm`
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
The point of concurrence of all angle bisectors of a triangle is called the ______.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

The longest chord of a circle is __________
The ______________ is the longest chord of a circle
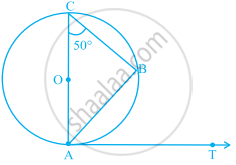
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
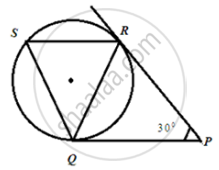
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
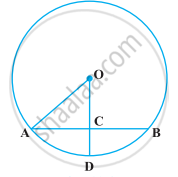
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
