Advertisements
Advertisements
Question
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
Solution
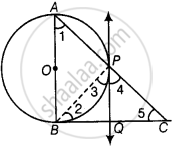
According to the question,
In a right angle ΔABC is which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P.
Also PQ is a tangent at P
To Prove: PQ bisects BC i.e. BQ = QC
Proof: ∠APB = 90° ...[Angle in a semicircle is a right-angle]
∠BPC = 90° ...[Linear Pair]
∠3 + ∠4 = 90° ...[1]
Now, ∠ABC = 90°
So in ΔABC
∠ABC + ∠BAC + ∠ACB = 180°
90° + ∠1 + ∠5 = 180°
∠1 + ∠5 = 90° ...[2]
Now, ∠1 = ∠3 ...[Angle between tangent and the chord equals angle made by the chord in alternate segment]
Using this in [2] we have
∠3 + ∠5 = 90° ...[3]
From [1] and [3] we have
∠3 + ∠4 = ∠3 + ∠5
∠4 = ∠5
QC = PQ ...[Sides opposite to equal angles are equal]
But also, PQ = BQ ...[Tangents drawn from an external point to a circle are equal]
So, BQ = QC
i.e. PQ bisects BC.
APPEARS IN
RELATED QUESTIONS
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

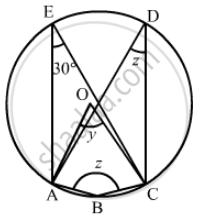
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Find the radius of the circle
Diameter = 30 cm
A line through the point of contact and passing through centre of the circle is known as ______
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
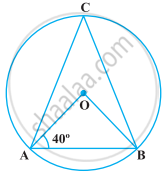
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

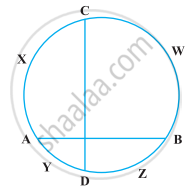
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.