Advertisements
Advertisements
Question
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
Solution
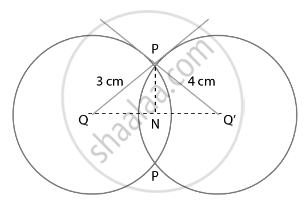
According to the question,
Two circles with centers O and O’ of radii 3 cm and 4 cm, respectively, intersect at two points P and Q, such that OP and O’P are tangents to the two circles and PQ is a common chord.
To Find: Length of common chord PQ
∠OPO’ = 90° ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
So OPO is a right-angled triangle at P
Using Pythagoras in ΔOPO’, we have
(OO’)2 = (O’P)2 + (OP)2
(OO’)2 = (4)2 + (3)2
(OO’)2 = 25
OO’ = 5 cm
Let ON = x cm and NO’ = 5 – x cm
In right angled triangle ONP
(ON)2 + (PN)2= (OP)2
x2 + (PN)2 = (3)2
(PN)2 = 9 – x2 ...[1]
In right angled triangle O’NP
(O’N)2 + (PN)2 = (O’P)2
(5 – x)2 + (PN)2 = (4)2
25 – 10x + x2 + (PN)2 = 16
(PN)2 = – x2+ 10x – 9 ...[2]
From [1] and [2]
9 – x2 = – x2 + 10x – 9
10x = 18
x = 1.8
From (1) we have
(PN)2 = 9 – (1.8)2
= 9 – 3.24
= 5.76
PN = 2.4 cm
PQ = 2PN
= 2(2.4)
= 4.8 cm
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
true or false
Sector is the region between the chord and its corresponding arc.
Prove that two different circles cannot intersect each other at more than two points.
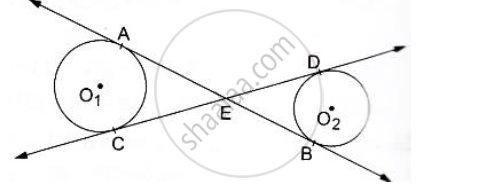
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
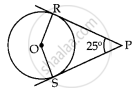
In the given figure, if ZRPS = 25°, the value of ZROS is ______
From the figure, identify the centre of the circle.