Advertisements
Advertisements
प्रश्न
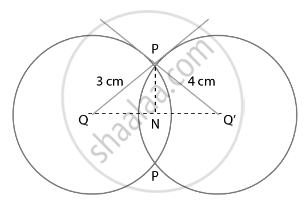
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
उत्तर
According to the question,
Two circles with centers O and O’ of radii 3 cm and 4 cm, respectively, intersect at two points P and Q, such that OP and O’P are tangents to the two circles and PQ is a common chord.
To Find: Length of common chord PQ
∠OPO’ = 90° ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
So OPO is a right-angled triangle at P
Using Pythagoras in ΔOPO’, we have
(OO’)2 = (O’P)2 + (OP)2
(OO’)2 = (4)2 + (3)2
(OO’)2 = 25
OO’ = 5 cm
Let ON = x cm and NO’ = 5 – x cm
In right angled triangle ONP
(ON)2 + (PN)2= (OP)2
x2 + (PN)2 = (3)2
(PN)2 = 9 – x2 ...[1]
In right angled triangle O’NP
(O’N)2 + (PN)2 = (O’P)2
(5 – x)2 + (PN)2 = (4)2
25 – 10x + x2 + (PN)2 = 16
(PN)2 = – x2+ 10x – 9 ...[2]
From [1] and [2]
9 – x2 = – x2 + 10x – 9
10x = 18
x = 1.8
From (1) we have
(PN)2 = 9 – (1.8)2
= 9 – 3.24
= 5.76
PN = 2.4 cm
PQ = 2PN
= 2(2.4)
= 4.8 cm
APPEARS IN
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
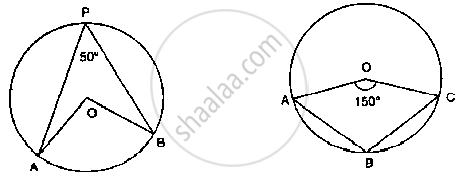
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
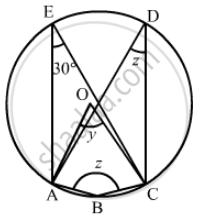
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
Draw circle with the radii given below.
2 cm
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]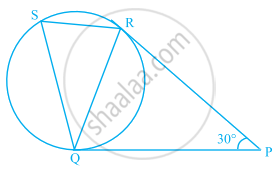
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.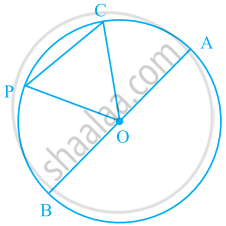
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.