Advertisements
Advertisements
प्रश्न
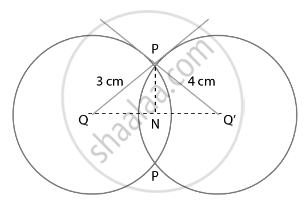
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
उत्तर
According to the question,
Two circles with centers O and O’ of radii 3 cm and 4 cm, respectively, intersect at two points P and Q, such that OP and O’P are tangents to the two circles and PQ is a common chord.
To Find: Length of common chord PQ
∠OPO’ = 90° ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
So OPO is a right-angled triangle at P
Using Pythagoras in ΔOPO’, we have
(OO’)2 = (O’P)2 + (OP)2
(OO’)2 = (4)2 + (3)2
(OO’)2 = 25
OO’ = 5 cm
Let ON = x cm and NO’ = 5 – x cm
In right angled triangle ONP
(ON)2 + (PN)2= (OP)2
x2 + (PN)2 = (3)2
(PN)2 = 9 – x2 ...[1]
In right angled triangle O’NP
(O’N)2 + (PN)2 = (O’P)2
(5 – x)2 + (PN)2 = (4)2
25 – 10x + x2 + (PN)2 = 16
(PN)2 = – x2+ 10x – 9 ...[2]
From [1] and [2]
9 – x2 = – x2 + 10x – 9
10x = 18
x = 1.8
From (1) we have
(PN)2 = 9 – (1.8)2
= 9 – 3.24
= 5.76
PN = 2.4 cm
PQ = 2PN
= 2(2.4)
= 4.8 cm
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
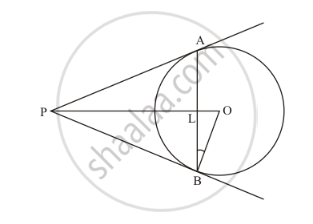
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
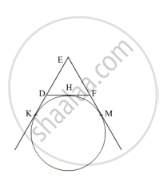
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
The point of concurrence of all angle bisectors of a triangle is called the ______.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Find the diameter of the circle
Radius = 8 cm
From the figure, identify a chord.

