Advertisements
Advertisements
प्रश्न
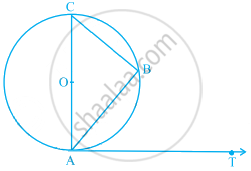
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
उत्तर
Since, AC is a diameter line, so angle in semi-circle an angle 90°.
∴ ∠ABC = 90° ...[By property]
In ∆ABC,
∠CAB + ∠ABC + ∠ACB = 180° ...[∵ Sum of all interior angles of any triangle is 180°]
⇒ ∠CAB + ∠ACB = 180° – 90° = 90° ...(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e., CA ⊥ AT
∴ ∠CAT = 90°
⇒ ∠CAB + ∠BAT = 90° ...(ii)
From equations (i) and (ii),
∠CAB + ∠ACB = ∠CAB + ∠BAT
⇒ ∠ACB = ∠BAT
Hence proved.
APPEARS IN
संबंधित प्रश्न
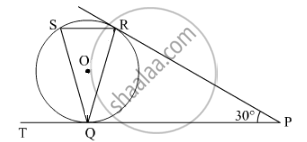
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
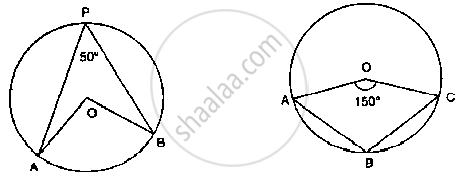
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Find the diameter of the circle
Radius = 6 cm
A line through the point of contact and passing through centre of the circle is known as ______
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.
From the figure, identify the centre of the circle.