Advertisements
Advertisements
प्रश्न
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

उत्तर
Given: ∠POR = 130°
So, ∠TSR = \[\frac{1}{2}\angle POR = \frac{1}{2} \times 130^o = 65^o = \angle2\] (Since angle subtended by the arc at the centre is double the angle subtended by it at the remaining part of the circle)
∠POQ = 180º − ∠POR = 180º − 130º = 50º .....(2) (Linear pair)
In
Δ POQ, \[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[Now \angle1 + \angle2 = 40^o + 65^o = 105^o\]
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
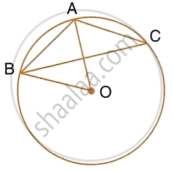
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
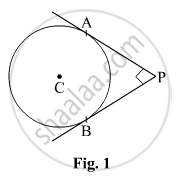
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
The ______________ is the longest chord of a circle
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.