Advertisements
Advertisements
प्रश्न
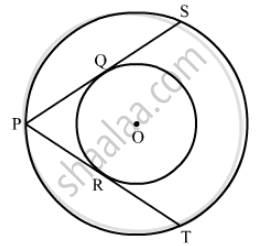
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
उत्तर
Given that PR = 5 cm.
PR and PQ are the tangents to the inner circle so,
PR = PQ = 5 cm (Tangents drawn from an external point to the circle are equal)
Now draw a perpendicular from the centre O to the tangent PS.
PS is the chord of the inner circle. we know that the perpendicular drawn
from the centre of the circle to the chord bisects the chord. So, PQ = QS = 5 cm
PS = PQ + QS = 5 cm + 5 cm = 10 cm
APPEARS IN
संबंधित प्रश्न
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
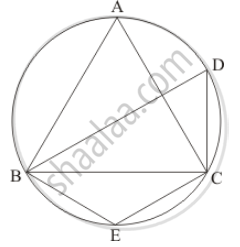
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
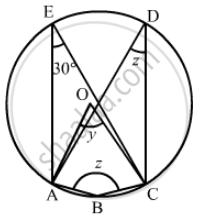
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
All the radii of a circle are _______________
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
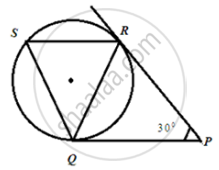
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]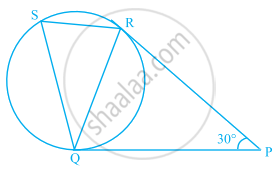
If an are subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is ______.
