Advertisements
Advertisements
प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
उत्तर

Suppose CD and AB are two parallel tangents of a circle with center O
Construction: Draw a line parallel to CD passing through O i.e. OP
We know that the radius and tangent are perpendicular at their point of contact.
∠OQC = ∠ORA = 90°
Now, ∠OQC + ∠POQ = 180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Similarly, Now, ∠ORA +∠POR =180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Now,∠POR + ∠POQ = 90° + 90° =180°
Since, ∠POR and ∠POQare linear pair angles whose sum is 180°
Hence, QR is a straight line passing through center O.
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
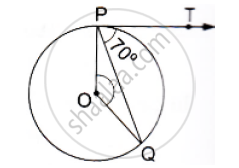
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

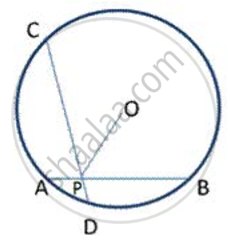
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
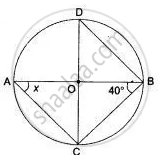
If O is the centre of the circle, find the value of x in each of the following figures
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
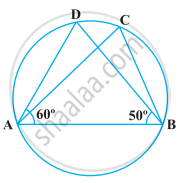
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
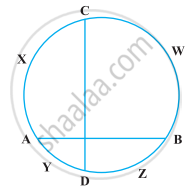
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.