Advertisements
Advertisements
प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
उत्तर

Suppose CD and AB are two parallel tangents of a circle with center O
Construction: Draw a line parallel to CD passing through O i.e. OP
We know that the radius and tangent are perpendicular at their point of contact.
∠OQC = ∠ORA = 90°
Now, ∠OQC + ∠POQ = 180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Similarly, Now, ∠ORA +∠POR =180° (co-interior angles)
⇒ ∠POQ = 180° - 90° = 90°
Now,∠POR + ∠POQ = 90° + 90° =180°
Since, ∠POR and ∠POQare linear pair angles whose sum is 180°
Hence, QR is a straight line passing through center O.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
true or false
The degree measure of an arc is the complement of the central angle containing the arc.
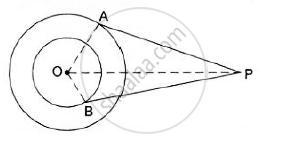
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

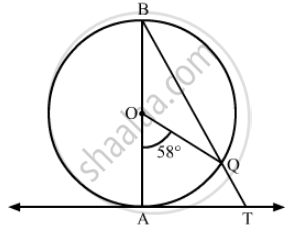
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
In the given figure, O is the centre of the circle. Name all radii of the circle.