Advertisements
Advertisements
प्रश्न
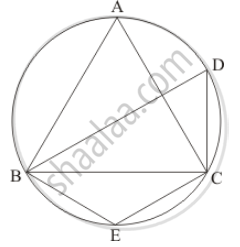
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
उत्तर
It is given that, ABC is an equilateral triangle
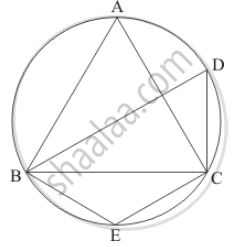
We have to find `angleBDC` and `angleBEC`
Since ΔABC is an equilateral triangle
So, `angleA = angleB = angleC = 60°`
And ABEC is cyclic quadrilateral
So `angle A + angle E = 180°` (Sum of opposite pair of angles of a cyclic quadrilateral is 180°.)
Then,
`angle E = 180° - 60°`
= 120°
Similarly BECD is also cyclic quadrilateral
So,
`angle E + angle D = 180°`
`angleD = 180° - 120°`
= 60°
Hence, `angle BDC `= 60° and `angle BEC = 120°`.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

Number of circles that can be drawn through three non-collinear points is
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.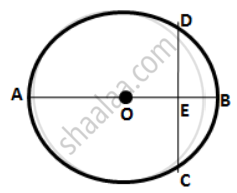
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.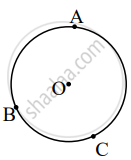
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.
Say true or false:
Two diameters of a circle will necessarily intersect.
