Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

उत्तर
In the given figure, let us join D an A.

Consider `ΔOCA`. We have,
OC = OA (Radii of the same circle)
We know that angles opposite to equal sides of a triangle will be equal. Therefore,
`∠OCA =∠OAC ` … (1)
It is clear from the figure that
`∠DCA +∠OCA=∠OCD`
Now from (1)
`∠DCA +∠OAC =∠OCD`
Now as BD is tangent therefore, `∠OCD=90^circ.`
Therefore `∠DCA +∠OAC = 90^circ`
From the figure we can see that `∠OAC =∠BAC`
`∠DAC + ∠BAC = 90^o`
Thus, we have proved.
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

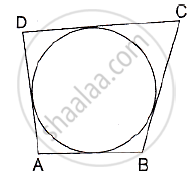
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
