Advertisements
Advertisements
प्रश्न
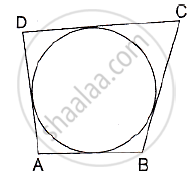
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
उत्तर
We know that when a quadrilateral circumscribes a circle then sum of opposites sides is equal to the sum of other opposite sides.
∴ AB + CD = AD+ BC
⇒ 6 + 8 = AD = 9
⇒ AD = 5 cm
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

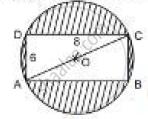
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
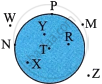 |
Find the diameter of the circle
Radius = 6 cm
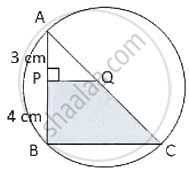
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.