Advertisements
Advertisements
प्रश्न
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
उत्तर
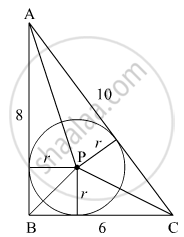
We have given that a circle is inscribed in a triangle
Using pythagoras theorem
`(AC)^2 = (AB)^2 + (BC)^2`
`(AC)^2 = (8)^2 + (6)^2`
`(AC)^2 = 64 + 36`
`(AC)^2 = 100`
⇒ AC = 10
Area of Δ ABC = area of Δ APB + area of Δ BPC + area of Δ APC
`1/2 xx b xx h = 1/2 xx b_1 xx h_1 + 1/2 xx b_2 xx h_2 + 1/2 xx b_3 xx h_3`
`1/2 xx 6 xx 8 = 1/2 xx 8 xx r + 1/2 xx 6 xx r + 1/2 xx 10 xx r`
`24 = 4r + 3r + 5r`
`24 = 12r`
⇒ r = 2
∵ d = 2r
⇒ `d = 2 xx 2`
⇒ d = 4 cm
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
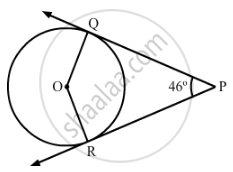
(A) 67°
(B) 134°
(C) 44°
(D) 46°
ture or false v
The degree measure of a semi-circle is 180°.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
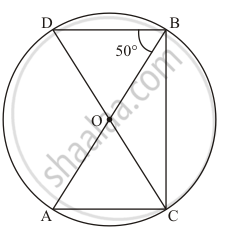
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Suppose you are given a circle. Describe a method by which you can find the center of this circle.
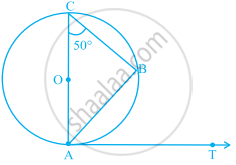
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
