Advertisements
Advertisements
प्रश्न
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
उत्तर
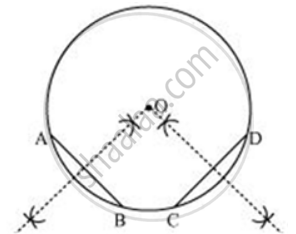
To draw the center of a given circle :
1. Draw the circle.
2. Take any two different chords AB and CD of this circle and draw perpendicular bisector of these chords.
3. let these perpendicular bisectors meet at point O.
So, O will be the center of the given circle.
APPEARS IN
संबंधित प्रश्न
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

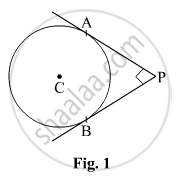
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.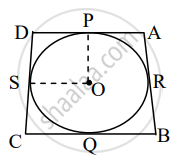
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
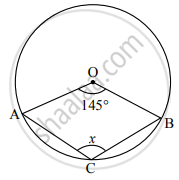
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.