Advertisements
Advertisements
प्रश्न
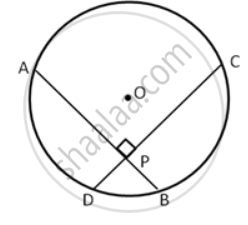
Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP
उत्तर
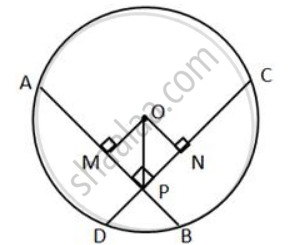
In ΔOMP and ΔONP,
OP = OP ...( common sides )
∠OMP = ∠ONP ...( both are right angles )
OM = OM ...( side both the chords are equal, so the distance of the chords from the centre are also equal )
ΔOMP ≅ ΔONP ...( RHS congruence criterion )
⇒ MP = PN ...(c.p.c.t ) ....( a )
(i) Since AB = CD ...( given )
⇒ AM = CN ...( drawn from the centre to the chord bisects the chord )
⇒ AM + MP = CN + NP .....( from a )
⇒ AP = CP ....( b )
(ii) Since AB = CD
⇒ AP + BP = CP + DP
⇒ BP = DP ....( from b )
Hence proved.
APPEARS IN
संबंधित प्रश्न
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
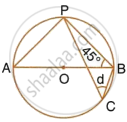
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
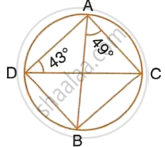
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
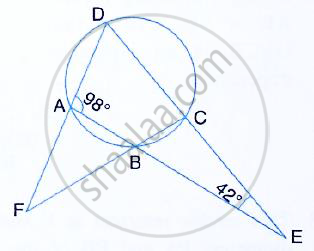
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
