Advertisements
Advertisements
प्रश्न
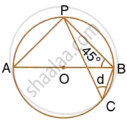
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
उत्तर

∠APB = 90° (Angle in a semicircle)
∴ ∠BAP = 90° – 45° = 45°
Now, d = ∠BCP = ∠BAP = 45°
(Angle subtended by the same chord on the circle are equal)
APPEARS IN
संबंधित प्रश्न
AB and CD are two equal chords of a circle with centre O which intersect each other at right
angle at point P. If OM⊥ AB and ON ⊥ CD; show that OMPN is a square.
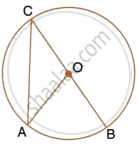
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
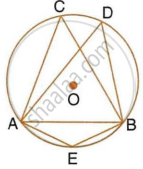
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
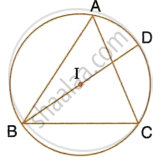
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
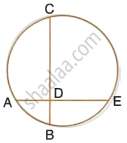
In the figure, chords AE and BC intersect each other at point D. If AD = BD, show that AE = BC.
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
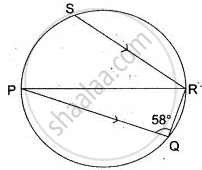
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)
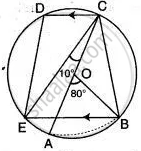
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.