Advertisements
Advertisements
प्रश्न
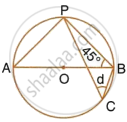
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
उत्तर

∠APB = 90° (Angle in a semicircle)
∴ ∠BAP = 90° – 45° = 45°
Now, d = ∠BCP = ∠BAP = 45°
(Angle subtended by the same chord on the circle are equal)
APPEARS IN
संबंधित प्रश्न
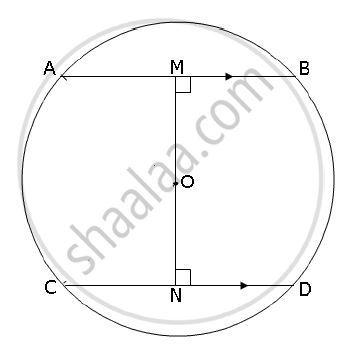
In the figure given below AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
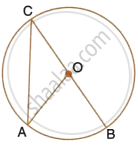
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
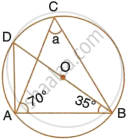
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
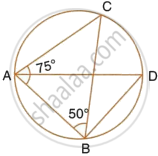
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
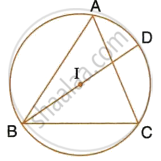
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
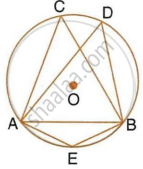
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
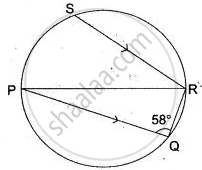
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)