Advertisements
Advertisements
प्रश्न
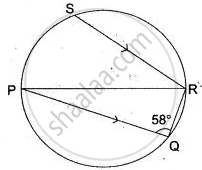
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)
उत्तर
(i) ∠ PRQ = 90° ...(∠in a semicircle)
In Δ PQR,
∠ RPQ + ∠ PQR + ∠ PRQ = 180° ....(∵ The sum of the three ∠s of a Δ is 180°)
⇒ ∠ RPQ + 58° + 90° = 180°
⇒ ∠ RPQ + 148° = 180°
⇒ ∠ RPQ = 180° - 148°
⇒ ∠ RPQ = 32°
(ii) ∵ PQ || SR and RP intersects them
∠ PRS = ∠ RPQ ...(Alternate angles)
∴ ∠ PRS = 32°
∵ PTSR is a cyclic quadrilateral.
∴ ∠ PTS + ∠ PRS = 180° ....( ∵ Opposite ∠s of a cyclic quadrilateral are supplementary)
⇒ ∠ PTS + 32° = 180°
⇒ ∠ PTS = 180° - 32° = 148°
⇒ ∠ STP = 148°.
APPEARS IN
संबंधित प्रश्न
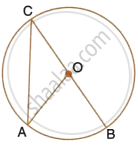
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
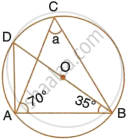
In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
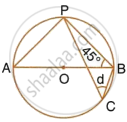
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
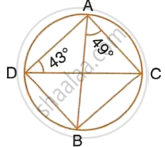
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
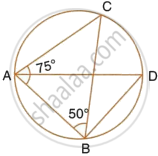
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
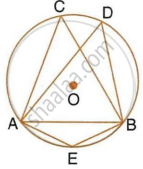
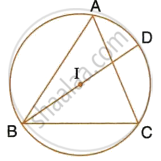
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
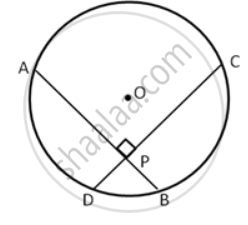
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP
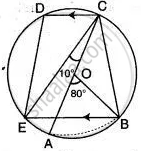
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.