Advertisements
Advertisements
प्रश्न
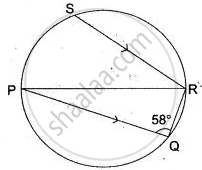
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)
उत्तर
(i) ∠ PRQ = 90° ...(∠in a semicircle)
In Δ PQR,
∠ RPQ + ∠ PQR + ∠ PRQ = 180° ....(∵ The sum of the three ∠s of a Δ is 180°)
⇒ ∠ RPQ + 58° + 90° = 180°
⇒ ∠ RPQ + 148° = 180°
⇒ ∠ RPQ = 180° - 148°
⇒ ∠ RPQ = 32°
(ii) ∵ PQ || SR and RP intersects them
∠ PRS = ∠ RPQ ...(Alternate angles)
∴ ∠ PRS = 32°
∵ PTSR is a cyclic quadrilateral.
∴ ∠ PTS + ∠ PRS = 180° ....( ∵ Opposite ∠s of a cyclic quadrilateral are supplementary)
⇒ ∠ PTS + 32° = 180°
⇒ ∠ PTS = 180° - 32° = 148°
⇒ ∠ STP = 148°.
APPEARS IN
संबंधित प्रश्न
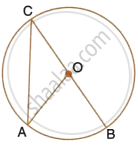
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
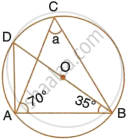
In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
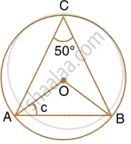
In the following figure, O is the centre of the circle. Find the values of a, b, c and d
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
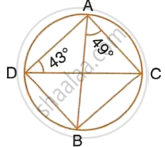
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
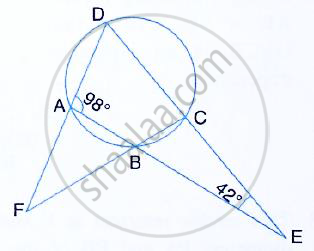
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.
AB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle.
