Advertisements
Advertisements
प्रश्न
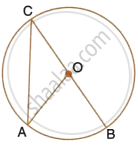
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
उत्तर

Here, ∠AOB = 2∠OCA ...(Angle at the center is double the angle at the circumference by the same chord)
`=>` ∠ACB =`70/2` = 35°
Now, OC = OA ...(Radii of same circle)
`=>` ∠OCA = ∠OAC = 35°
APPEARS IN
संबंधित प्रश्न
AB and CD are two equal chords of a circle with centre O which intersect each other at right
angle at point P. If OM⊥ AB and ON ⊥ CD; show that OMPN is a square.
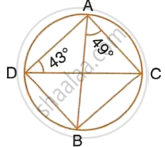
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
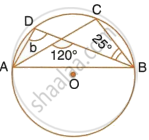
In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
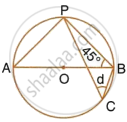
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
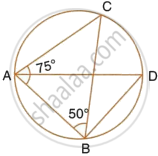
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP
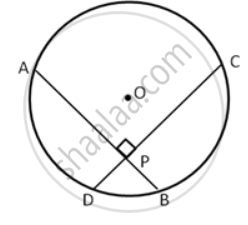
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
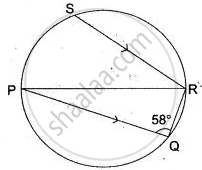
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)
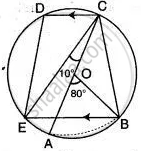
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.