Advertisements
Advertisements
प्रश्न
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
उत्तर
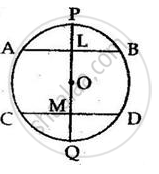
Given: AB and CD are the two chords of a circle with center O.
L and M are the mid-points of AB and CD and O lies in the line joining ML.
To prove: AB || CD.
Proof:
AB and CD are two chords of a circle with center O.
Line LOM bisects them at L and M.
Then, OL ⊥ AB
and, OM ⊥ CD
∴ ∠ALM = ∠LMD = 90°
But they are alternate angles
∴ AB || CD.
APPEARS IN
संबंधित प्रश्न
In the following figure, O is the centre of the circle. Find the values of a, b and c.

In the following figure, O is the centre of the circle. Find the values of a, b, c and d.
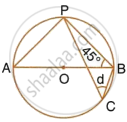
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
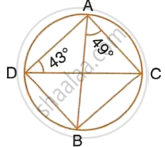
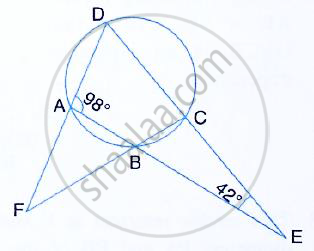
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
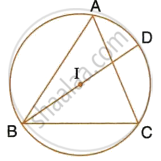
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
Given two equal chords AB and CD of a circle with center O, intersecting each other at point P.
Prove that:
(i) AP = CP
(ii) BP = DP
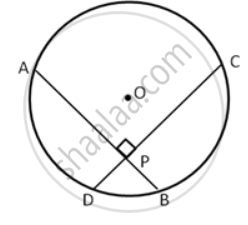
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
Two chords AB, CD of lengths 16 cm and 30 cm, are parallel. If the distance between AB and CD is 23 cm. Find the radius of the circle.
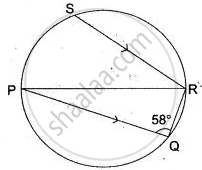
In the adjoining figure, PQ is the diameter, chord SR is parallel to PQ. Give ∠ PQR = 58°.
Calculate:
(i) ∠ RPQ,
(ii) ∠ STP ( T is a point on the minor arc)
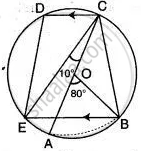
In the diagram given alongside, AC is the diameter of the circle, with centre O. CD and BE are parallel. ∠ AOB = 80° and ∠ ACE = 10°. Calculate: (i) ∠ BEC (ii) ∠ BCD (iii) ∠ CED.