Advertisements
Advertisements
Question
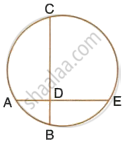
The line joining the midpoints of two chords of a circle passes through its center.
Prove that the chords are parallel.
Solution
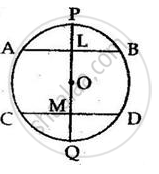
Given: AB and CD are the two chords of a circle with center O.
L and M are the mid-points of AB and CD and O lies in the line joining ML.
To prove: AB || CD.
Proof:
AB and CD are two chords of a circle with center O.
Line LOM bisects them at L and M.
Then, OL ⊥ AB
and, OM ⊥ CD
∴ ∠ALM = ∠LMD = 90°
But they are alternate angles
∴ AB || CD.
APPEARS IN
RELATED QUESTIONS
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
- ∠OCA,
- ∠OAC.
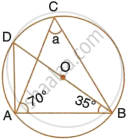
In the following figure, O is the centre of the circle. Find the value of a, b, c and d.
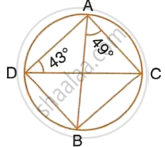
Calculate:
- ∠CDB,
- ∠ABC,
- ∠ACB.
In the following figure, O is centre of the circle and ΔABC is equilateral.
Find:
- ∠ADB,
- ∠AEB.
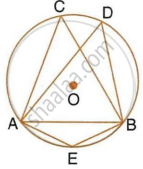
Given: ∠CAB = 75° and ∠CBA = 50°. Find the value of ∠DAB + ∠ABD.
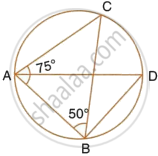
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; Calculate :
(i) ∠AFB (ii) ∠ADC
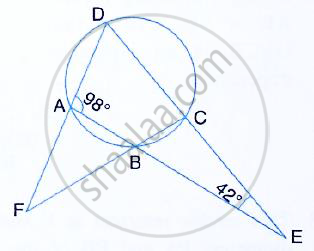
In the given figure, I is the incentre of ΔABC. BI when produced meets the circumcircle of ΔABC at D. ∠BAC = 55° and ∠ACB = 65°; calculate:
- ∠DCA,
- ∠DAC,
- ∠DCI,
- ∠AIC.
In following fig., chords PQ and RS of a circle intersect at T. If RS = 18cm, ST = 6cm and PT = 18cm, find the length of TQ.

In the figure, chords AE and BC intersect each other at point D. If AD = BD, show that AE = BC.
If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
