Advertisements
Advertisements
Question
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles.
Show that:
(i) AB = CD ;
(ii) AC = BD.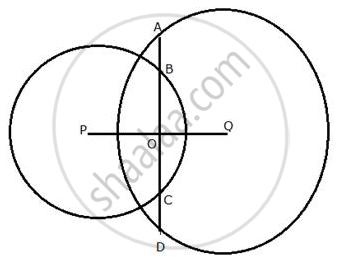
Solution
In the circle with center Q, QO ⊥ AD
∴ OA = OD ...(i) ...[perpendicular drawn the center of a circle to a chord bisects it]
In circle with center P, PO ⊥ BC
∴ OB = OC ....(ii) ....[perpendicular drawn the center of a circle to a chord bisects it]
(i) - (ii) gives,
AB = CD ...(iii)
(ii) Adding BC to both sides of equation (iii)
AB + BC + CD + BC
⇒ AC = BD
APPEARS IN
RELATED QUESTIONS
A chord of length 8 cm is drawn at a distance of 3 cm from the centre of a circle. Calculate the radius of the circle.
The radius of a circle is 17.0 cm and the length of perpendicular drawn from its centre to a chord is 8.0 cm. Calculate the length of the chord.
In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centres of
the circles. Show that:
(i) AB = CD,
(ii) AC = BD.

Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
In the following figure, a circle is inscribed in the quadrilateral ABCD.

If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
A chord CD of a circle whose center is O is bisected at P by a diameter AB. Given OA = OB = 15 cm and OP = 9 cm.
Calculate the lengths of: (i) CD ; (ii) AD ; (iii) CB.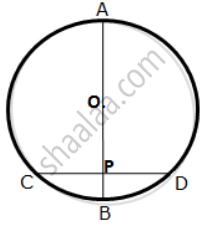
A chord of length 8 cm is drawn at a distance of 3 cm from the center of the circle.
Calculate the radius of the circle.
The radius of a circle is 13 cm and the length of one of its chords is 24 cm.
Find the distance of the chord from the center.
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.
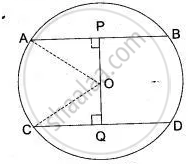
In Fig. O is the centre of the circle of radius 5 cm. OP ⊥ AB, OQ ⊥ CD, AB || CD, AB = 6 cm and CD = 8 cm. Determine PQ.

