Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
рдЙрддреНрддрд░
Let the two circles intersect at points X and Y.
XY is the common chord.
Suppose ‘A’ is a point on the common chord and AM and AN be the tangents drawn A to the circle
We need to show that AM = AN.
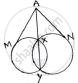
In order to prove the above relation, following property will be used.
“Let PT be a tangent to the circle from an external point P and a secant to the circle through
P intersects the circle at points A and B, then ЁЭСГЁЭСЗ2 = ЁЭСГЁЭР┤ × ЁЭСГЁЭР╡"
Now AM is the tangent and AXY is a secant ∴ ЁЭР┤ЁЭСА2 = ЁЭР┤ЁЭСЛ × ЁЭР┤ЁЭСМ … . . (ЁЭСЦ)
AN is a tangent and AXY is a secant ∴ ЁЭР┤ЁЭСБ2 = ЁЭР┤ЁЭСЛ × ЁЭР┤ЁЭСМ … . . (ЁЭСЦЁЭСЦ)
From (i) & (ii), we have ЁЭР┤ЁЭСА2 = ЁЭР┤ЁЭСБ2
∴ AM = AN
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
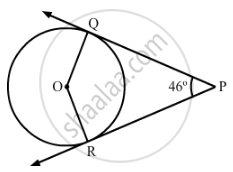
(A) 67°
(B) 134°
(C) 44°
(D) 46°
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
Fill in the blank
A continuous piece of a circle is ............... of the circle
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.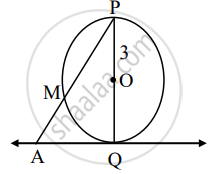
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
