Advertisements
Advertisements
प्रश्न
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.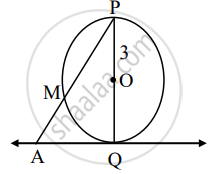
उत्तर
Given: line AQ is a tangent.
OP = 3, m(arc PM) = 120°
To find: AP
In the given figure, arc PMQ is a semicircle.
∴ m(arc PMQ) = 180° ......[Measure of semicircular arc is 180°]
∴ m(arc PM) + m(arc MQ) = 180° .....[Arc addition property]
∴ 120° + m(arc MQ) = 180° ......[Given]
∴ m(arc MQ) = 180° – 120°
∴ m(arc MQ) = 60° .......(i)
∠MPQ = `1/2` m(arc MQ) .....[Inscribed angle theorem]
∴ ∠MPQ = `1/2 xx 60^circ` ......[From (i)]
∴ ∠MPQ = 30°
i.e., ∠APQ = 30° ......(ii) [A – M – P]
In ∆PQA, ∠PQA = 90° ......[Tangent theorem]
∠ APQ = 30° ......[From (ii)]
∴ ∠PAQ = 60° ......[Remaning angle of ∆PQA]
∴ ∆PAQ is 30° – 60° – 90° triangle.
∴ PQ = `sqrt(3)/2` AP ......[Side opposite to 60°]
∴ (PO + OQ) = `sqrt(3)/2` AP ......[P – O – Q]
∴ (3 + 3) = `sqrt(3)/2` AP ......[Radii of same circle and op = 3]
∴ AP = `(6 xx 2)/sqrt(3)`
∴ AP = `(6 xx 2 xx sqrt(3))/(sqrt(3) xx sqrt(3))` ......[Multiply and divide by `sqrt(3)`]
∴ AP = `(6 xx 2 xx sqrt(3))/3`
∴ AP = `2 xx 2sqrt(3)`
∴ AP = `4sqrt(3)` units
APPEARS IN
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
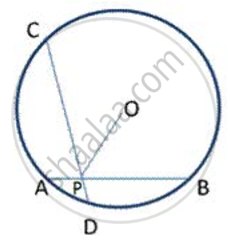
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Can the length of a chord of a circle be greater than its diameter ? Explain.
If O is the center of the circle in the figure alongside, then complete the table from the given information.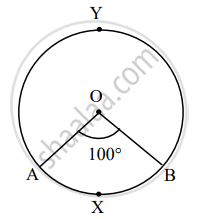
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
A line through the point of contact and passing through centre of the circle is known as ______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
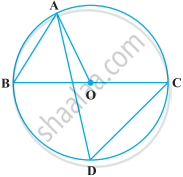
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
