Advertisements
Advertisements
प्रश्न
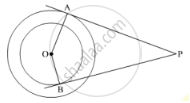
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
उत्तर
In triangle BOA,
OB = OA ...[Both are the radius of circle]
∠OAB = ∠OBA ...(i) [Angle opposite to equal sides are equal]
Now, In triangle OAB,
∠OBA + ∠AOB + ∠AOC = 180° ...[By angle sum property of a triangle]
∠OAB + ∠OAB + 90° = 180° ...[From equation (i)]
2∠OAB = 180° – 90°
2∠OAB = 90°
∠OAB = 45°
Again, in triangle AOC,
AO = OC ...[Radii or circle]
∠OCA = ∠OAC ...(ii) [Angle opposite to equal sides are equal]
Now, by angle sum property of a triangle,
∠AOC + ∠OAC + ∠OCA = 180°
150° + 2∠OAC = 180° ...[From equation (ii)]
2∠OAC = 180° – 150°
2∠OAC = 30°
∠OAC = 15°
∠BAC = ∠OAB + ∠OAC = 45° + 15° = 60°
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
Find the radius of the circle
Diameter = 76 cm
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
