Advertisements
Advertisements
प्रश्न

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
उत्तर
The solution is not available
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
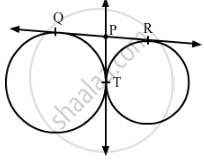
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
ture or false v
The degree measure of a semi-circle is 180°.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
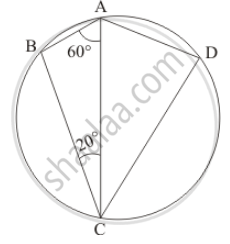
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

Use the figure given below to fill in the blank:
________ is a radius of the circle.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
Draw circle with the radii given below.
4 cm
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
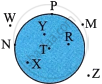 |
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
A line segment which joins any two points on a circle is a ___________
Find the diameter of the circle
Radius = 6 cm
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
