Advertisements
Advertisements
प्रश्न
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
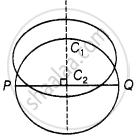
We draw two circle with centre C1 and C2 passing through the endpoint P and Q at a line segment PQ.
We know, that perpendicular bisectors of a chord of a circle always passes through the centre of circle.
Thus, perpendicular bisector of PQ passes through C1 and C2.
Similarly, all the circle passing through PQ will have their centre on perpendiculars bisectors of PQ.
APPEARS IN
संबंधित प्रश्न
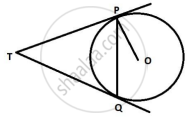
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
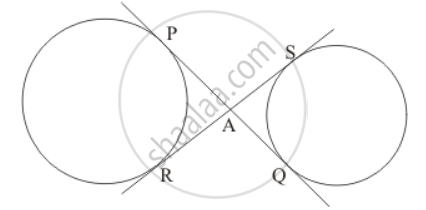
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
All the radii of a circle are _______________
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
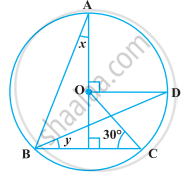
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.