Advertisements
Advertisements
प्रश्न
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
उत्तर
Steps of Construction:
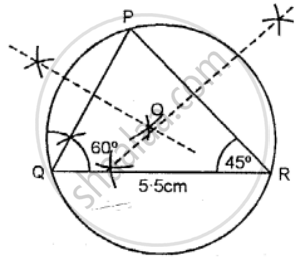
(i) Draw a ∆PQR in which QR = 5.5 cm, ∠Q = 60° and ∠R = 45°.
(ii) Draw the arc bisector of PQ and PR which intersect at O.
(iii) Taking O as center and radius OP or OQ or OR draw a circle.
This circle will pass through vertices P, Q, and R.
APPEARS IN
संबंधित प्रश्न
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
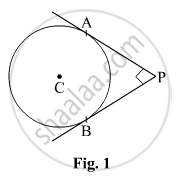
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
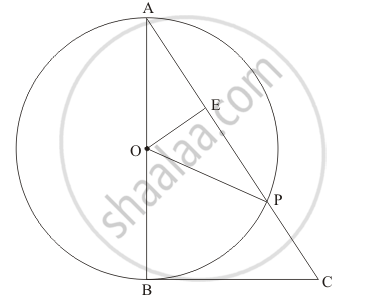
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
All the radii of a circle are _______________
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.