Advertisements
Advertisements
प्रश्न
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
पर्याय
60°
45°
30°
15°
उत्तर
We will associate the given information in the following figure.
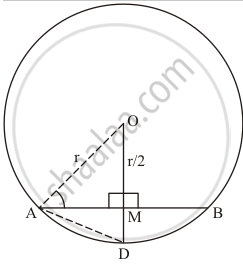
Since AO = r (radius of circle)
AM = `r/2` (given)
Extended OM to D where MD = `r/2`
Consider the triangles AOM and triangle AMD
OM = MD
`angleAMO = angle AMD` = 90°
AM = AM (common Sides
So by SSS property
Δ AMO ≅ Δ DM
So AD = AO = r and OD=OM+MD=r
Hence ΔAOD is equilateral triangle
So `angle OAD` = 60°
We know that in equilateral triangle altitudes divide the vertex angles
Therefore `angleOAM = (angleOAD)/2`
`=60/2`
= 30°
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Prove that two different circles cannot intersect each other at more than two points.
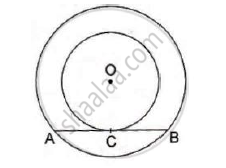
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Find the radius of the circle
Diameter = 30 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
Is every chord of a circle also a diameter?
