Advertisements
Advertisements
प्रश्न
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
उत्तर
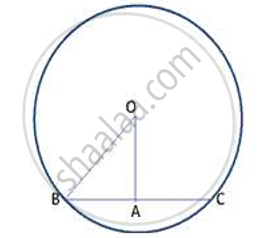
BA = AC ----(1) (Perpendicular from centre to a chord bisects the chord)
In right Δ OAB,
By Pythagoras theorem, OB2 = OA2 + AB2
AB2 = 6.52 + 2.52
= 42.25 - 6.25 = 36
AB = 6cm
∴ Length of chord BC = 2 AB (from (1))
= 2 (6) = 12 cm
APPEARS IN
संबंधित प्रश्न
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
If O is the centre of the circle, find the value of x in each of the following figures
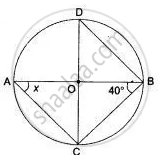
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

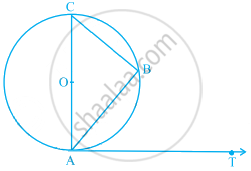
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
Say true or false:
Two diameters of a circle will necessarily intersect.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
