Advertisements
Advertisements
प्रश्न
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
पर्याय
70°
100°
125°
150°
उत्तर
70°
It is given that ABCD is cyclic quadrilateral ∠ADB = 90° and ∠DCA = 80°. We have to find ∠DAB
We have the following figure regarding the given information
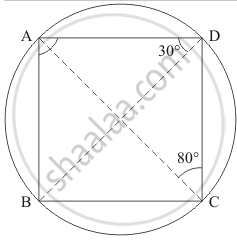
∠BDA = ∠BCA = 30° (Angle in the same segment are equal)
Now, since ABCD is a cyclic quadrilateral
So, ∠DAB + ∠BCD = 180°
`angleDAB + angleBCA + angleDCA` = 180°
`angleDAB ` + 30° + 80° = 180°
`angleDAB` = 180° - 110°
`angleDAB ` = 70 °
APPEARS IN
संबंधित प्रश्न
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in BC || AD, ∠ADC = 110° and ∠BAC = 50°. Find ∠DAC.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.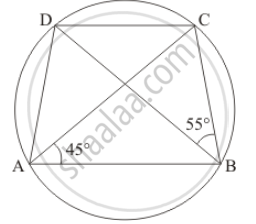
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
