Advertisements
Advertisements
प्रश्न
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
उत्तर
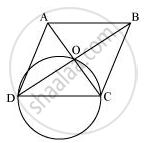
Let ABCD be a rhombus in which diagonals are intersecting at point O and a circle is drawn while taking side CD as its diameter. We know that a diameter subtends 90° on the arc.
∴ ∠COD = 90°
Also, in rhombus, the diagonals intersect each other at 90°.
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Clearly, point O has to lie on the circle.
APPEARS IN
संबंधित प्रश्न
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
In a cyclic quadrilateral ABCD, if ∠A − ∠C = 60°, prove that the smaller of two is 60°
ABCD is a cyclic quadrilateral in ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.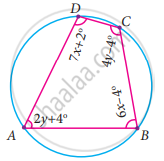
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
