Advertisements
Advertisements
प्रश्न
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
उत्तर
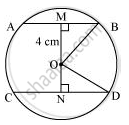
Let AB and CD be two parallel chords in a circle centered at O. Join OB and OD.
Distance of smaller chord AB from the centre of the circle = 4 cm
OM = 4 cm
MB = AB/2 = 6/2 = 3cm
In ΔOMB,
OM2 + MB2 = OB2
(4)2 + (3)2 = OB2
16 + 9 = OB2
OB2 = 25
`OB = sqrt25`
OB = 5cm
In ΔOND,
OD = OB = 5cm (Radii of the same circle)
ND = CD/2 = 8/2 = 4cm
ON2 + ND2 = OD2
ON2 + (4)2 = (5)2
ON2 = 25 - 16 = 9
ON = 3
Therefore, the distance of the bigger chord from the centre is 3 cm.
APPEARS IN
संबंधित प्रश्न
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
Find all the angles of the given cyclic quadrilateral ABCD in the figure.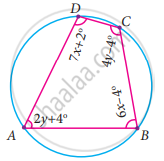
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
