Question

In the given figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = 77°, AC and BD intersect at P. Then, find ∠DPC.

Answer 1

In a cyclic quadrilateral it is known that the opposite angles are supplementary, meaning that the opposite angles add up to 180° .

Here we have a cyclic quadrilateral ABCD. The centre of this circle is given as ‘O’.

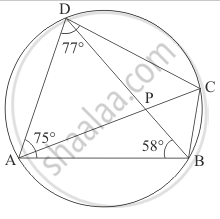
Since in a cyclic quadrilateral the opposite angles are supplementary, here

`angleADC + angleABD + angle CBD ` = 180°

                                 `angleCBD = 180° - angleADC - angleABD `       

                                              = 180° - 77° - 58° 

                                 `angle CBD ` = 45°

Whenever a chord is drawn in a circle two segments are formed. One is called the minor segment while the other is called the major segment. The angle that the chord forms with any point on the circumference of a particular segment is always the same.

Here, ‘CD’ is a chord and ‘A’ and ‘B’ are two points along the circumference on the major segment formed by the chord ‘CD’.

So, `angleCBD = angleCAD ` = 45°

Now,

`angleBAD = angleBAC + angleCAD `

`angleBAC = angleBAD - angleCAD`

              = 75° - 45°

 `angleBAC` =  30°

In any triangle the sum of the interior angles need to be equal to 180°.

Consider the triangle ΔABP,

\[\angle PAB + \angle ABP + \angle APB = 180°\]
\[ \Rightarrow \angle APB = 180°- 30°- 58°\]
\[ \Rightarrow \angle APB = 92°\]

From the figure, since ‘AC’ and ‘BD’ intersect at ‘P’ we have,

`angle APB = angleDPC  ` = 92° 

Hence the measure of `angleDPC `  is92° .