Advertisements
Advertisements
प्रश्न
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are `90^@-1/2A, 90^@-1/2B" and "90^@-1/2C`
उत्तर

It is given that BE is the bisector of ∠B.
∴ ∠ABE = ∠B/2
However, ∠ADE = ∠ABE (Angles in the same segment for chord AE)
⇒ ∠ADE = ∠B/2
Similarly, ∠ACF = ∠ADF = ∠C/2 (Angle in the same segment for chord AF)
∠D = ∠ADE + ∠ADF
`=(angleB)/2 + (angleC)/2`
`=1/2(angleB+angleC)`
`=1/2(180^@-angleA)`
`=90^@-1/2angleA`
Similarly, it can be proved that
`angleE=90^@-1/2angleB`
`angleF=90^@-1/2angleC`
APPEARS IN
संबंधित प्रश्न
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
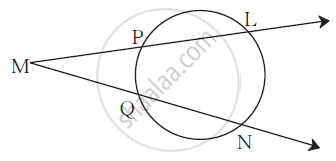
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC =

If P, Q and R are the mid-points of the sides BC, CA and AB of a triangle and AD is the perpendicular from A on BC, prove that P, Q, R and D are concyclic.
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
