Advertisements
Advertisements
प्रश्न
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
उत्तर
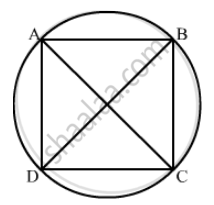
To prove: AC = BD
Proof: We know that equal chords subtend equal at the centre of circle and the angle subtended by a chord at the centre is twice the angle subtended by it at remaining part of the circle.
\[\angle AOD = \angle BOC \left( \text{ O is the centre of the circle } \right)\]
\[\angle AOD = 2\angle ACD \]
\[\text{ and } \angle BOC = 2\angle BDC\]
\[\text{ Since, } \angle AOD = \angle BOC\]
\[ \Rightarrow \angle ACD = \angle BDC . . . . . \left( 1 \right) \]
\[\angle ACB = \angle ADB . . . . . \left( 2 \right) \left( \text{ Angle in the same segment are equal } \right)\]
\[\text{ Adding } \left( 1 \right) \text{ and } \left( 2 \right)\]
\[\angle BCD = \angle ADC . . . . . \left( 3 \right)\]
\[\text{ In } \bigtriangleup ACD \text{ and } \bigtriangleup BDC\]
\[CD = CD \left( \text{ common } \right)\]
\[\angle BCD = \angle ADC \left[ \text{ Using } \left( 3 \right) \right]\]
\[AD = BC \left( given \right)\]
\[\text{ Hence } , \bigtriangleup ACD \cong BDC \left( \text{ SAS congruency criterion } \right)\]
\[ \therefore AC = BD \left( \text{ cpct } \right)\]
Hence Proved
APPEARS IN
संबंधित प्रश्न
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

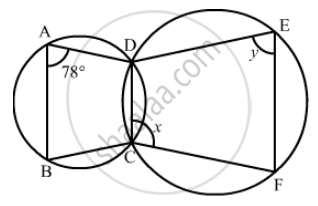
In the given figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.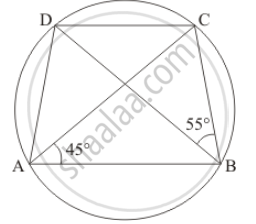
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that AD || BC .
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

ABCD is a cyclic quadrilateral. M (arc ABC) = 230°. Find ∠ABC, ∠CDA, and ∠CBE.
In a cyclic quadrilaterals ABCD, ∠A = 4x, ∠C = 2x the value of x is
If non-parallel sides of a trapezium are equal, prove that it is cyclic.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
